拓扑排序

定义

拓扑排序（Topological Sorting）是针对有向无环图（DAG, Directed Acyclic Graph）所有顶点的线性序列的一种排序方法。

其目的是将图中的所有顶点排成一个线性序列，使得对于图中的每一条有向边 u->v，顶点 u 在 v 之前。

有向无环图（DAG）才有拓扑排序，非DAG图没有拓扑排序一说。

DAG必须满足下面两个条件

每个顶点出现且只出现一次。
若存在一条从顶点 A 到顶点 B 的路径，那么在序列中顶点 A 出现在顶点 B 的前面。

概述

拓扑排序常用于解决任务调度、编译顺序确定、依赖关系解析等问题。其本质是寻找一种可行的线性排序，使得满足依赖关系的任务得以按顺序执行。

拓扑排序的前提是图必须是有向无环图（DAG），否则无法进行拓扑排序。常见的拓扑排序方法包括入度法（Kahn算法）和深度优先搜索（DFS）法。

算法思想

入度法（Kahn算法）

统计所有顶点的入度。

将所有入度为 0 的顶点加入队列。

依次从队列中取出顶点 u，将其加入拓扑序列，并移除 u 指向的所有边。

若某个顶点的入度变为 0，将其加入队列。

重复上述过程，直到队列为空。

若最终拓扑序列中的顶点数等于图中顶点数，则排序成功，否则说明存在环。

深度优先搜索（DFS）法

维护一个访问标记数组 vis，其中 0 表示未访问，1 表示正在访问，2 表示已访问。

遍历所有未访问的顶点，执行 DFS 过程。

在 DFS 过程中，若访问到正在访问的顶点，则说明存在环。

若 DFS 递归回溯，则将当前顶点加入拓扑序列。

逆序输出拓扑序列。

算法复杂度

拓扑排序的两种主要实现算法（Kahn 算法和 DFS 递归算法）在时间和空间复杂度上既有相同之处，也存在细微差异，具体分析如下：

一、时间复杂度对比

两种算法在所有场景下的时间复杂度均为 O (V + E)，其中 V 是顶点数，E 是边数。

Kahn 算法：
- 需要遍历所有边来计算入度（O (E)）
- 每个顶点会入队、出队一次（O (V)）
- 每个边会被处理一次（减少邻接顶点的入度，O (E)）
- 总操作次数为 O (V + E)
- 最好情况：图中只有顶点无 edges（E=0），此时只需遍历所有顶点（O (V)），总复杂度 O (V) = O (V + E)。
- 平均情况：任意有向无环图（DAG），需遍历所有顶点（O (V)）和所有边（O (E)），总复杂度 O (V + E)。
- 最坏情况：图为线性链（如 0→1→2→…→V-1），此时需处理所有顶点和边，复杂度仍为 O (V + E)。
DFS 递归算法：
- 需要遍历所有顶点（每个顶点被访问一次，O (V)）
- 需要遍历所有边（每个边被检查一次，O (E)）
- 递归过程中对顶点的压栈、出栈操作总次数为 O (V)
- 总操作次数为 O (V + E)
- 最好情况：图中无 edges（E=0），每个顶点仅被访问一次（O (V)），总复杂度 O (V) = O (V + E)。
- 平均情况：任意 DAG，需遍历所有顶点（O (V)）和每条边（O (E)），总复杂度 O (V + E)。
- 最坏情况：图为星形结构（一个顶点指向所有其他顶点），仍需遍历所有顶点和边，复杂度 O (V + E)。

二、空间复杂度对比

两种算法的空间复杂度均与图的存储方式和顶点数量相关，整体为 O(V + E)，但具体构成略有不同：

1. Kahn 算法的空间复杂度：O (V + E)

邻接表存储图：O (V + E)（存储所有顶点和边）
入度数组：O (V)（记录每个顶点的入度）
队列存储：最坏情况下需要存储所有顶点（如线性链结构），O (V)
结果列表：O (V)
总空间：O (V + E)

2. DFS 递归算法的空间复杂度：O (V + E)

邻接表存储图：O (V + E)
递归调用栈：最坏情况下（如线性链结构）深度为 V，O (V)
访问标记数组：O (V)
结果列表（逆序存储）：O (V)
总空间：O (V + E)

三、特殊场景下的差异

Kahn 算法：队列的空间开销在顶点入度分布均匀时较小，适合处理大型稀疏图。
DFS 递归算法：递归栈深度可能成为瓶颈（如 V=10^5 时会栈溢出），实际应用中常需改为非递归实现（空间复杂度不变，但避免栈溢出）。

总结

算法	最好时间复杂度	平均时间复杂度	最坏时间复杂度	空间复杂度（所有场景）
Kahn 算法	O(V + E)	O(V + E)	O(V + E)	O(V + E)
DFS 算法	O(V + E)	O(V + E)	O(V + E)	O(V + E)

关键结论

两种算法的时间和空间复杂度完全相同，均由顶点数和边数共同决定，选择时主要考虑实际场景（如是否需要检测环、实现难度、图的稠密程度等）。
复杂度与图的具体结构（如是否为链状、星形等）无关，因为无论何种 DAG，都必须遍历所有顶点和边。
实际选择算法时，更多考虑工程实现（如 Kahn 算法适合处理动态入度变化，DFS 算法适合检测环并排序），而非复杂度差异。

分析

理解拓扑排序的核心障碍，往往不在于 “看了多少资料”，而在于是否打通了 “概念定义→实际意义→算法逻辑→应用场景” 的链路 —— 很多资料只侧重其中某一环（比如只讲算法步骤），导致知识碎片化，难以串联成可理解的整体。下面我们从 “拆解核心问题” 的角度，一步步帮你建立完整的认知框架。

一、先破题：拓扑排序不是 “排序”，是 “依赖关系的线性化”

首先要纠正一个常见误解：拓扑排序（Topological Sorting）不是对 “数值大小” 或 “字母顺序” 的排序，而是对「有向无环图（DAG）」中 “节点依赖关系” 的梳理 —— 本质是把 “谁必须在谁之前完成” 的规则，转化为一个合法的线性执行顺序。

举个最直观的例子：大学选课。

图的 “节点”= 课程（如《高数》《线代》《概率论》）；
图的 “有向边”= 先修关系（如《高数》→《线代》，表示 “先学高数才能学线代”；《高数》→《概率论》，表示 “先学高数才能学概率论”）；
拓扑排序的结果 = 一份合法的选课顺序（比如 [《高数》→《线代》→《概率论》] 或 [《高数》→《概率论》→《线代》]，两种都合法，因为线代和概率论之间没有依赖关系）。

如果没有这个 “依赖关系” 的认知基础，直接看 “入度”“出度”“删边” 等算法术语，就会像看无意义的符号操作。

二、再扎根：必须先明确拓扑排序的 “前提” 和 “目标”

拓扑排序不是所有图都能做，也不是只有唯一结果，这两个前提不明确，后续理解会一直卡壳：

1. 前提：只适用于「有向无环图（DAG）」

为什么 “有向”？因为依赖关系是单向的（“先学 A 再学 B” 不能反过来）；
为什么 “无环”？如果有环（比如 “A 必须先学 B，B 必须先学 A”），就会陷入 “先有鸡还是先有蛋” 的死循环，不可能存在合法的线性顺序（这也是拓扑排序的核心判断：能做拓扑排序 ↔ 图是 DAG）。

反例：如果课程里有《线代》→《高数》，同时《高数》→《线代》，就形成了环，这两门课永远无法安排顺序，自然没有拓扑排序。

2. 目标：输出一个 “满足所有依赖关系” 的线性序列

这个序列需要满足：对于图中每一条有向边 u→v，u 在序列中都必须排在 v 的前面。注意：拓扑排序的结果不唯一—— 只要满足依赖关系，不同的顺序都是合法的。比如上面的选课例子，线代和概率论谁先谁后都可以，因为它们之间没有依赖。

三、拆算法：两种核心方法的 “直觉逻辑”（比代码更重要）

资料里常讲的 “Kahn 算法（入度表法）” 和 “ DFS 深度优先搜索法”，本质都是围绕 “如何找到‘无前置依赖’的节点，逐步拆解图” 展开的，关键是理解 “每一步操作的意义”，而不是死记步骤。

方法 1：Kahn 算法（入度表法）—— 像 “剥洋葱”，从 “无依赖节点” 开始

Kahn 算法是实现拓扑排序的一种具体算法，它本质上是一种基于 BFS（广度优先搜索）的拓扑排序方法。

适用场景不同

BFS 是一种通用的图遍历算法，可用于任何图（有向 / 无向、有环 / 无环），目的是按层次遍历节点。
Kahn 算法仅适用于有向无环图（DAG），专门用于解决拓扑排序问题。

核心思想不同

BFS 的核心是 "先访问当前节点，再依次访问其所有邻接节点"，通过队列控制访问顺序。
Kahn 算法的核心是 "每次选择入度为 0 的节点，移除该节点并减少其邻接节点的入度"，本质上是通过 BFS 框架实现拓扑排序。

数据结构的特殊处理

Kahn 算法在 BFS 基础上增加了入度（in-degree）的概念：
初始化时，所有入度为 0 的节点入队（这些节点没有前驱依赖）。
每次出队一个节点后，将其所有邻接节点的入度减 1，若某节点入度变为 0，则入队。
最终若输出的节点数等于图中总节点数，则完成拓扑排序；否则图中存在环。

“入度” 是理解这个算法的关键：一个节点的入度 = 指向它的边的数量（比如《线代》的入度是 1，因为只有《高数》→《线代》这一条边指向它；《高数》的入度是 0，因为没有先修课）。

算法逻辑完全贴合 “现实做事顺序”，比如你安排任务时，肯定先做 “不需要等别人” 的事：

计算所有节点的入度，把 “入度为 0” 的节点（无前置依赖）加入「队列」（比如先把《高数》放进队列）；
从队列中取出一个节点，把它加入「拓扑序列」（确定 “先做这件事”）；
删掉这个节点所有的出边（比如删掉《高数》→《线代》、《高数》→《概率论》），并更新对应节点的入度（《线代》入度从 1 变 0，《概率论》入度从 1 变 0）；
把新的 “入度为 0” 的节点（现在是《线代》和《概率论》）加入队列；
重复步骤 2-4，直到队列为空。
最后检查：如果拓扑序列的长度 = 图中节点总数 → 排序成功（图是 DAG）；否则 → 图有环，排序失败。

例子演示（选课图）：

初始入度：高数 (0)、线代 (1)、概率论 (1) → 队列：[高数]
取 “高数” 入序列 → 删边后，线代 (0)、概率论 (0) → 队列：[线代，概率论]
取 “线代” 入序列 → 删边（线代无出边）→ 队列：[概率论]
取 “概率论” 入序列 → 队列空
序列：[高数，线代，概率论]（合法）；若第二步取 “概率论”，则序列为 [高数，概率论，线代]（也合法）。

方法 2：DFS 法 —— 像 “走迷宫”，先找 “没有后续依赖” 的节点

DFS 法的核心思路是 “逆序构建序列”：先递归找到 “所有后续节点都处理完” 的节点（比如 “没有后续课” 的课程），再把它加入序列的前面 —— 因为 “后续节点要在它之后，所以它要排在序列的前面”。

具体逻辑（结合选课例子）：

选一个未访问的节点（比如先选《线代》）；
递归访问它的所有 “前置依赖节点”（《线代》的前置是《高数》，所以先递归处理《高数》）；
处理《高数》时，发现它没有前置依赖（无未访问的前置节点），就把《高数》加入「临时序列」；
回到《线代》，发现所有前置都处理完了，把《线代》加入临时序列；
再选未访问的《概率论》，递归处理其前置《高数》（已访问），把《概率论》加入临时序列；
最后把临时序列「反转」，得到拓扑序列：[高数，线代，概率论]（或其他合法顺序）。

关键直觉：DFS 是 “从后往前” 找依赖 —— 先确定 “最后能做的事”，再倒推 “之前该做什么”，最后反转得到 “从前往后的顺序”。

下面用图形直观感受：

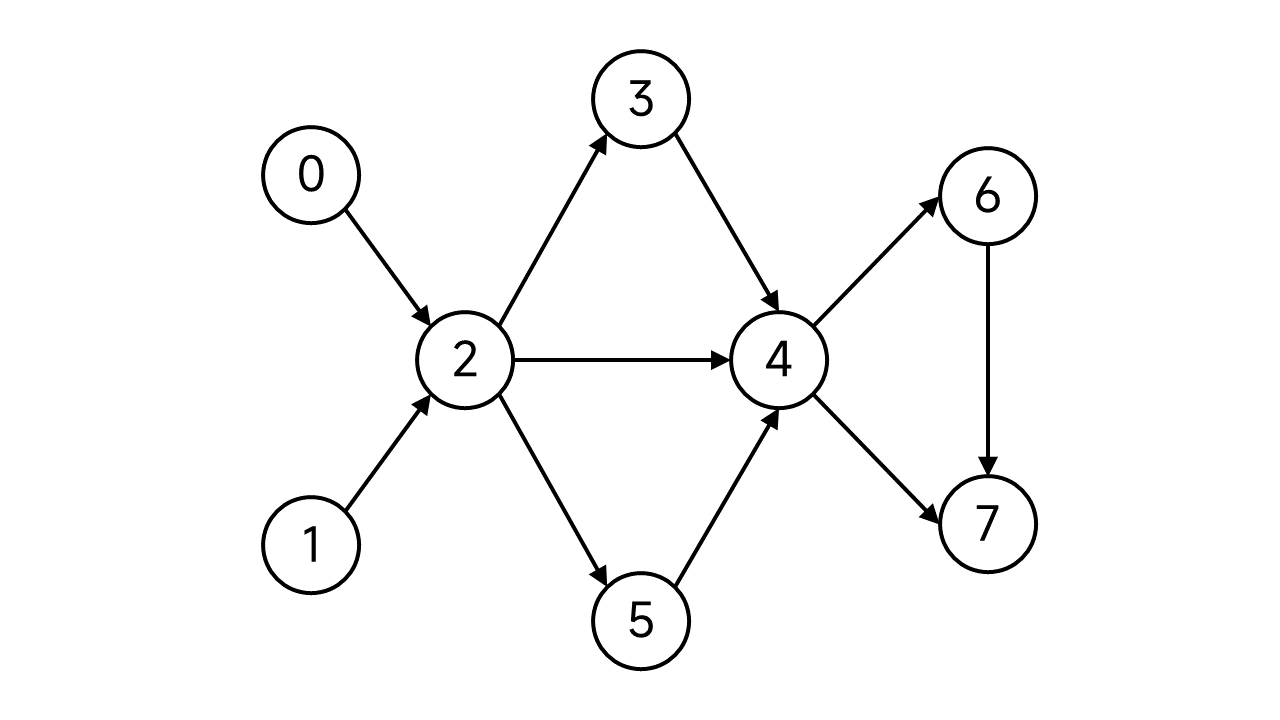
首先，我们需要维护一个栈，用来存放DFS到的节点。另外规定每个节点有两个状态：已访问（这里用蓝绿色表示）、未访问（这里用黑色表示）。

任选一个节点开始DFS，比如这里就从0开始。

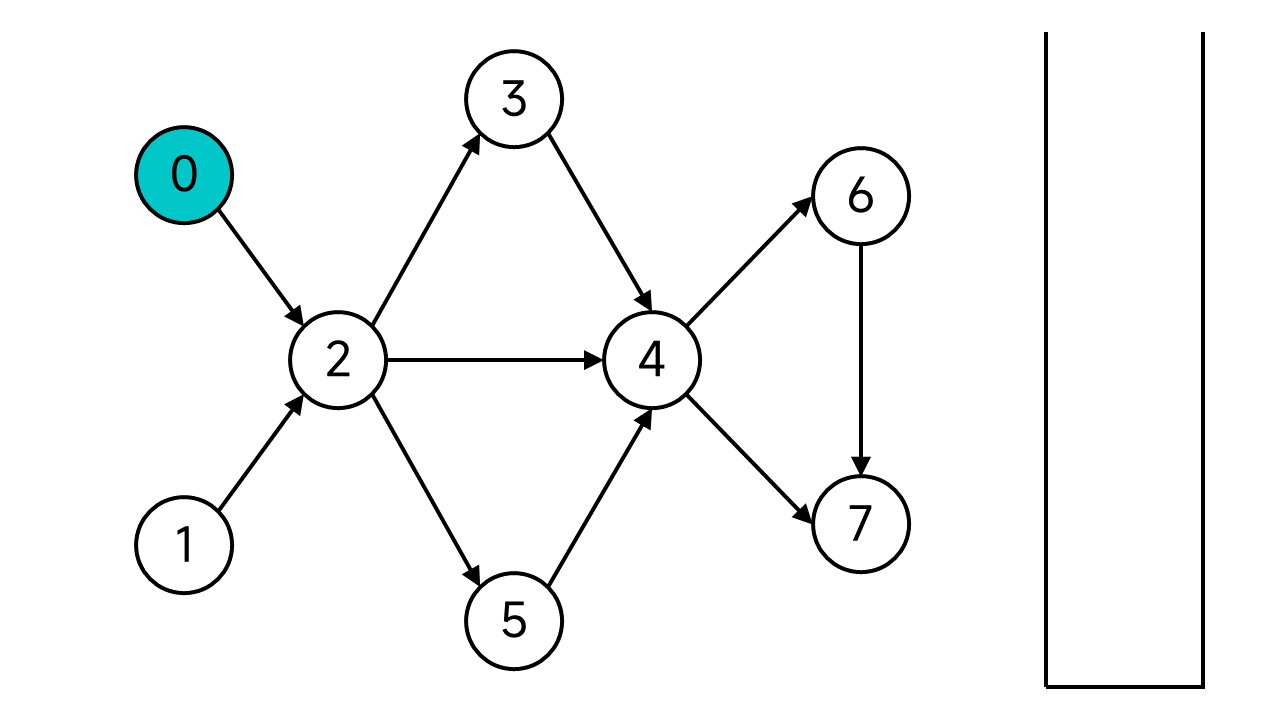
首先将节点0的状态设为已访问，然后节点0的邻居（节点0的出边指向的节点）共有1个：节点2，它是未访问状态，于是顺下去访问节点2。

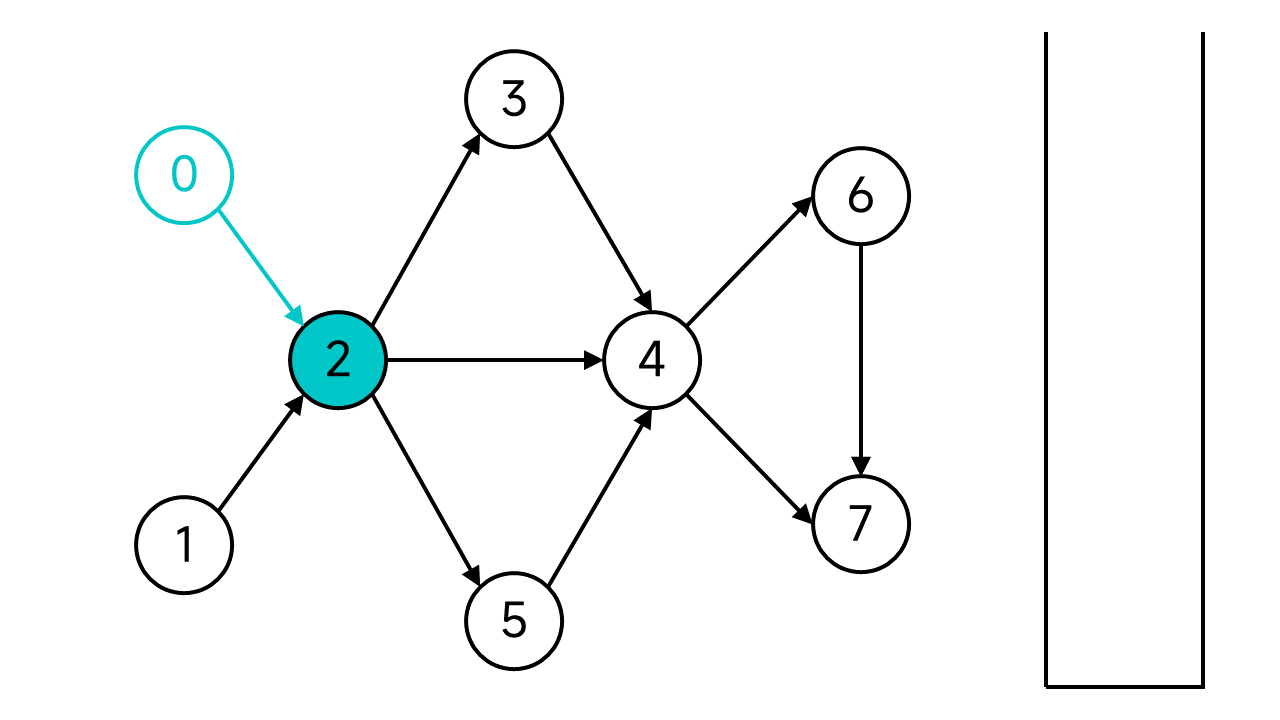
节点2的状态也设为已访问。节点2有3个邻居：3、4、5，都是未访问状态，不妨从3开始。一直这样访问下去，直到访问到没有出边的节点7。

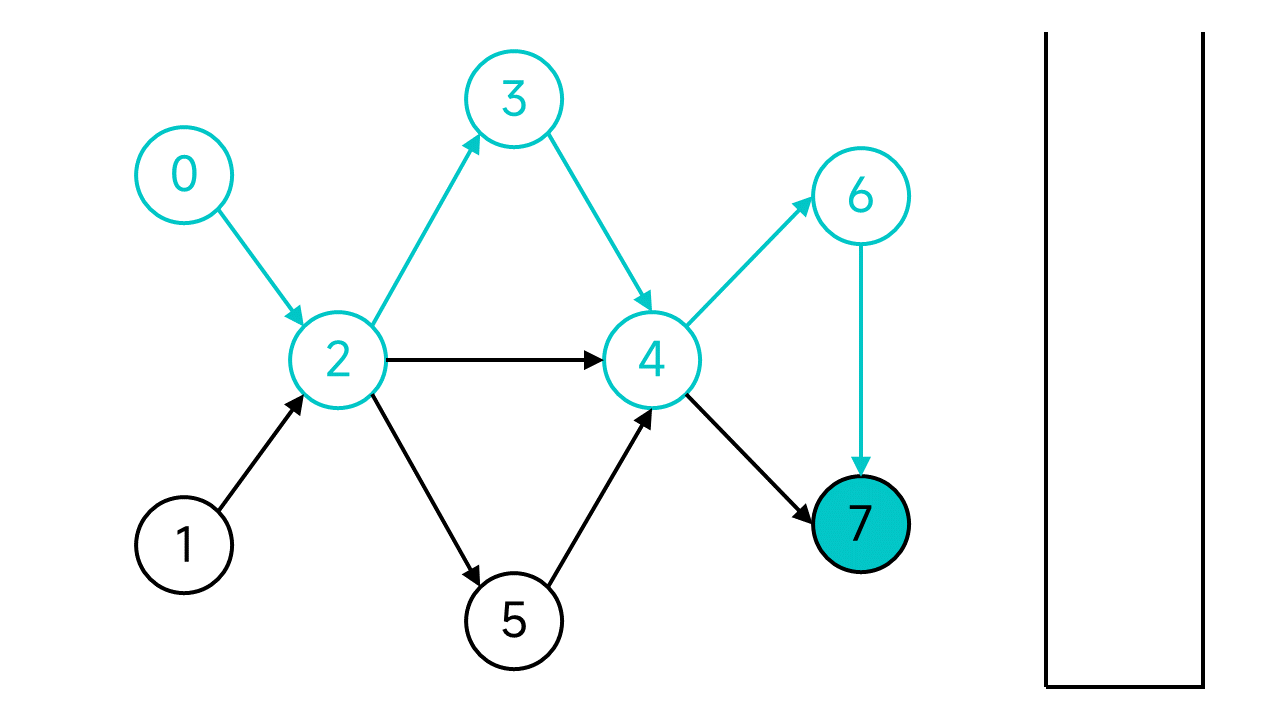
节点7没有出边了，这时候就将节点7入栈。

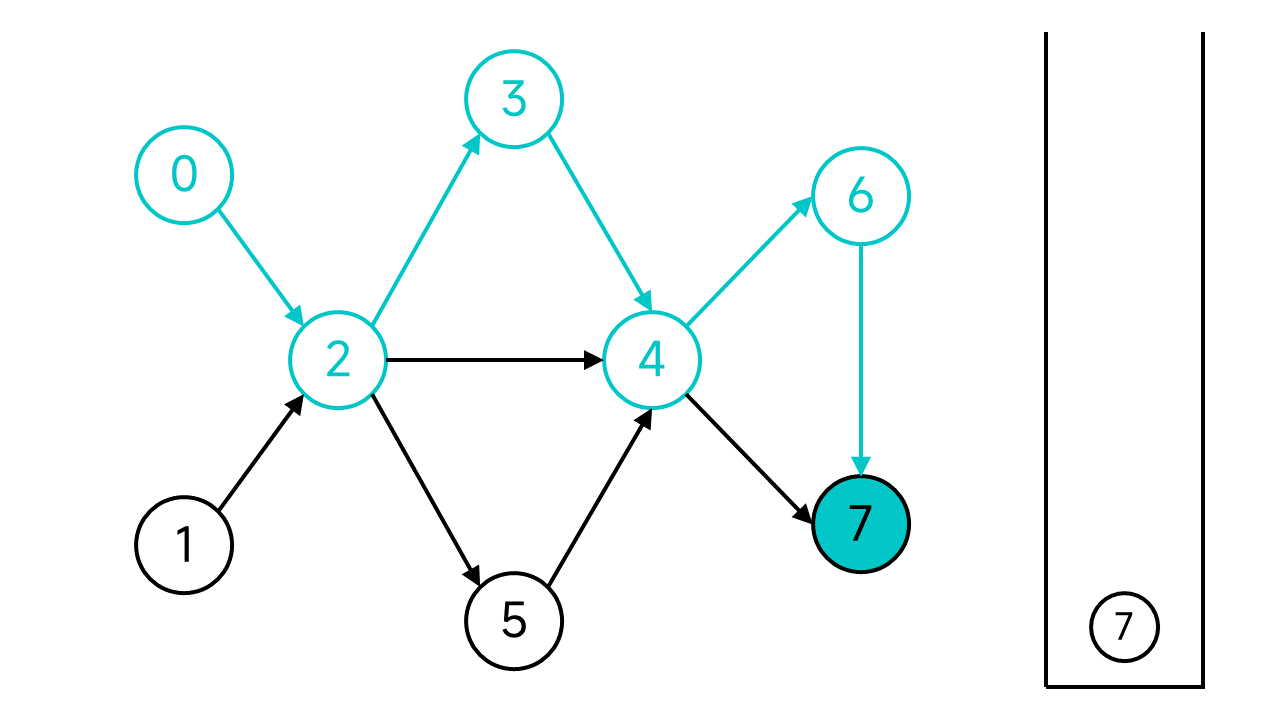
退回到节点6，虽然6还有邻居，但是唯一的邻居节点7是已访问状态，也入栈。再次退回，节点4的两个邻居也都已访问，依旧入栈并后退。以此类推，退回到节点2。

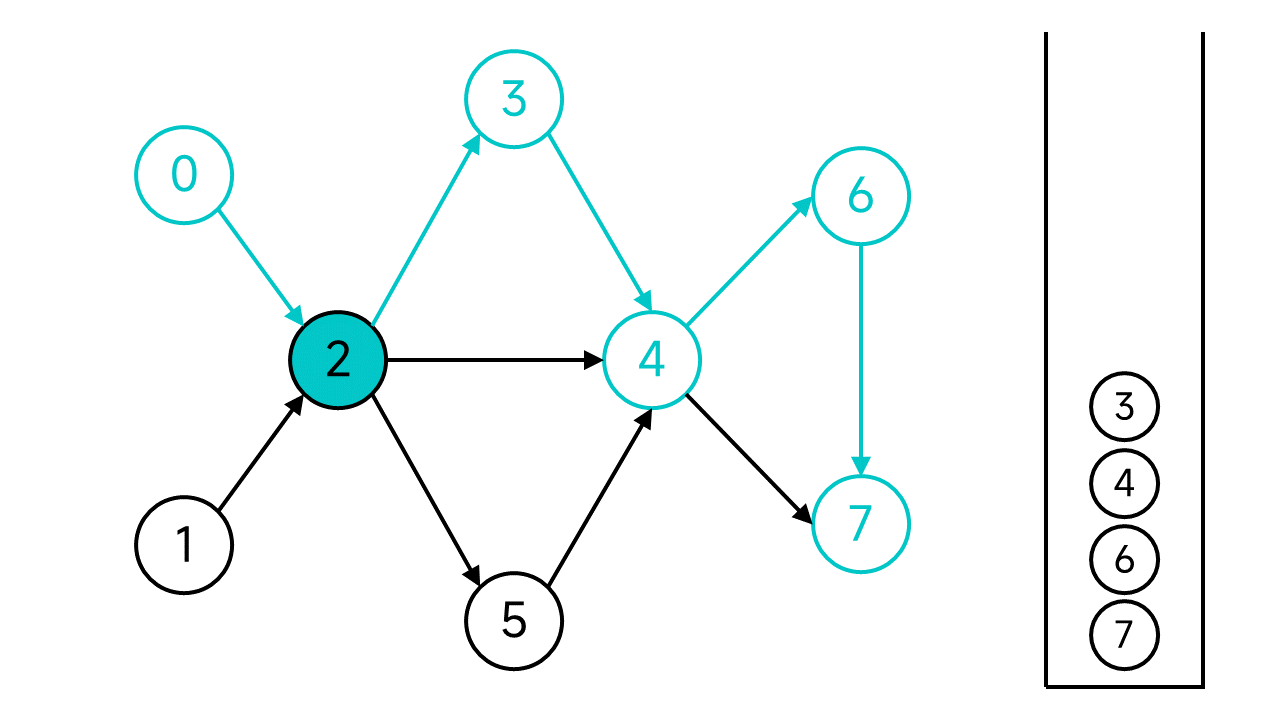
节点2有3个邻居，其中节点3和4已访问，但是节点5还未访问，访问节点5。

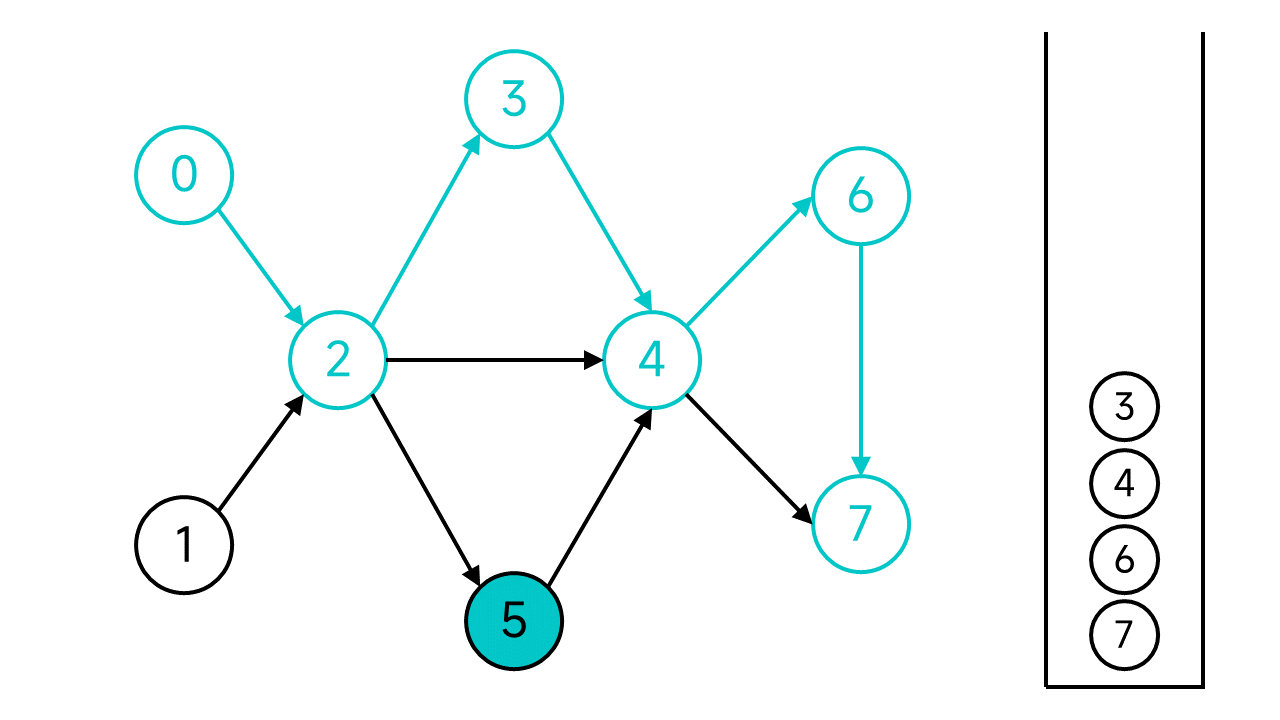
接下来的步骤是一样的，不再赘述了，直接退回到节点0并将0入栈。

现在，从节点0开始的DFS宣告结束，但是图中还有未访问的节点：节点1，从节点1继续开始DFS。

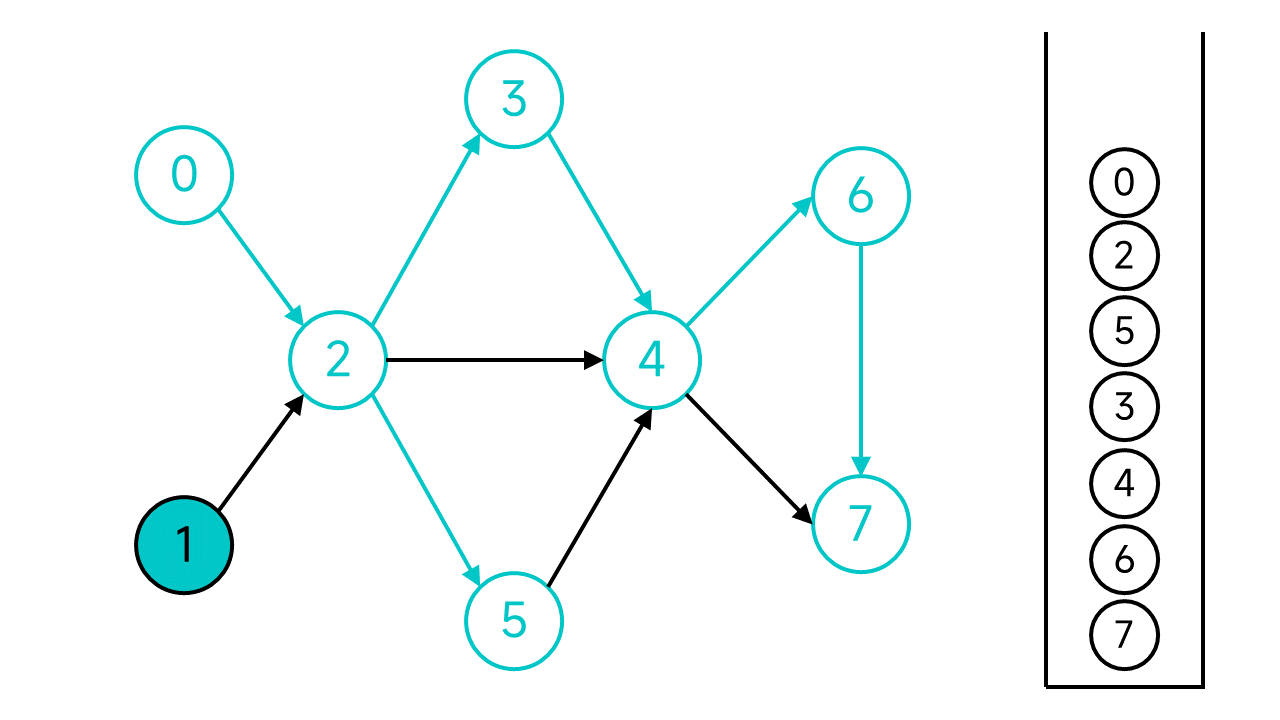
节点1的邻居节点2已经访问过了，直接将节点1入栈。

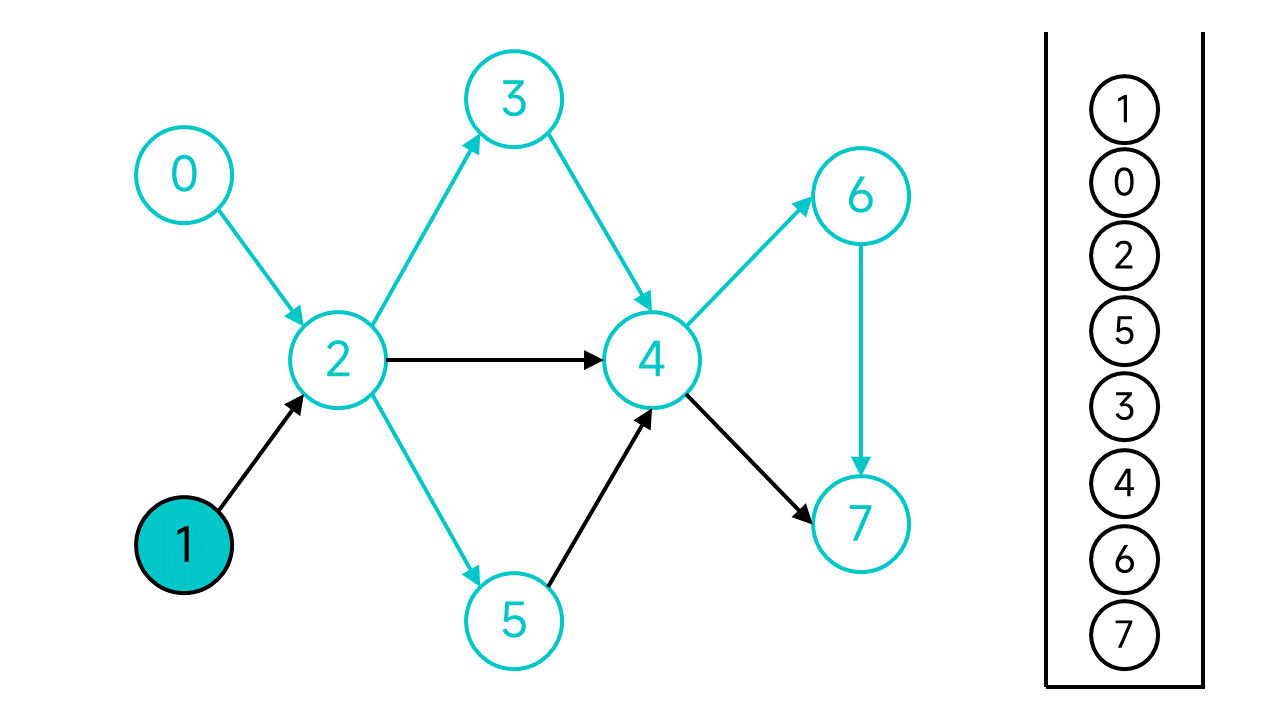
至此，整个DFS过程宣告结束。从栈顶到栈底的节点序列1 0 2 5 3 4 6 7就是整个图的一个拓扑排序序列。

四、找场景：用 “实际问题” 验证理解

如果能把拓扑排序和具体场景绑定，理解会更扎实。除了选课，常见场景还有：

项目排期：节点 = 任务，边 =“任务 A 完成后才能做任务 B”（如 “需求评审→开发→测试”）；
编译依赖：节点 = 源文件，边 =“文件 A 依赖文件 B 的定义”（编译器需要按拓扑顺序编译）；
食谱步骤：节点 = 烹饪步骤，边 =“步骤 A 完成后才能做步骤 B”（如 “切菜→炒菜”）。

试着用这些场景套 Kahn 算法：比如项目排期里，“需求评审” 是入度 0 的节点，先做它；做完后删边，“开发” 入度变 0，再做开发…… 这样就把抽象算法和具体做事逻辑对齐了。

五、避坑：常见误区总结（帮你自查卡壳点）

误区 1：“拓扑排序是唯一的”→ 错，只要满足依赖，顺序可多样；
误区 2：“所有图都能做拓扑排序”→ 错，只有 DAG 可以，有环图不行；
误区 3：“入度 / 出度是抽象概念”→ 错，入度就是 “需要等多少个前置节点”，出度就是 “有多少个后置节点”；
误区 4：“算法步骤记不住”→ 别记步骤，记 “剥洋葱（Kahn）” 或 “倒推依赖（DFS）” 的直觉，步骤会自然推导出来。

最后：验证理解的小练习

如果上面的内容看下来有感觉，试着做一个小验证：假设有一个图：节点 A、B、C、D，边为 A→B，A→C，B→D，C→D。

这是 DAG 吗？（是，无环）；
用 Kahn 算法求拓扑序列：初始入度 A (0)、B (1)、C (1)、D (2) → 队列先加 A；取 A 后，B (0)、C (0) 入队；取 B 后，D (1)；取 C 后，D (0)；取 D → 序列可以是 [A,B,C,D] 或 [A,C,B,D]；
用 DFS 法求：递归 D 的前置 B 和 C，B 的前置 A，C 的前置 A → 临时序列是 [D,B,C,A] 或 [D,C,B,A]，反转后就是合法序列。

如果能独立完成这个练习，说明你已经打通了拓扑排序的核心逻辑 —— 接下来再看资料里的代码实现（比如用邻接表存图、队列实现 Kahn），就会明白 “代码只是把直觉逻辑翻译成机器语言”，而不是一堆看不懂的指令了。

代码

import java.util.*;

public class TopologicalSort {

    // 图的表示：邻接表
    private int V; // 顶点数量
    private List<List<Integer>> adj; // 邻接表

    // 构造函数
    public TopologicalSort(int v) {
        V = v;
        adj = new ArrayList<>(v);
        for (int i = 0; i < v; i++) {
            adj.add(new ArrayList<>());
        }
    }

    // 添加边
    public void addEdge(int u, int v) {
        adj.get(u).add(v);
    }

    /**
     * Kahn算法实现拓扑排序
     * 思路：基于入度的算法，不断选择入度为0的节点
     * 0->1, 0->2, 1->3, 2->3, 3->4
     */
    public List<Integer> topologicalSortKahn() {
        // 计算每个节点的入度 [0,0,0,0,0]
        int[] inDegree = new int[V];
        for (int u = 0; u < V; u++) {
            // u:4 节点4没有数据，进不来循环
            for (int v : adj.get(u)) {
                // u:0 v:1 [0,1,0,0,0]
                // u:0 v:2 [0,1,1,0,0]
                // u:1 v:3 [0,1,1,1,0]
                // u:2 v:3 [0,1,1,2,0]
                // u:3 v:4 [0,1,1,2,1]
                inDegree[v]++;
            }
        }

        // 将所有入度为0的节点加入队列
        Queue<Integer> queue = new LinkedList<>();
        for (int i = 0; i < V; i++) {
            // 只有节点0的入度为0
            if (inDegree[i] == 0) {
                queue.add(i);
            }
        }

        // 存储拓扑排序结果
        List<Integer> result = new ArrayList<>();

        // 处理队列中的节点
        while (!queue.isEmpty()) {
            // 入度为0的节点
            int u = queue.poll();
            result.add(u);

            // 减少相邻节点的入度
            for (int v : adj.get(u)) {
                inDegree[v]--;
                // u:0 - v:1 [0,0,1,2,1]
                // u:0 - v:2 [0,0,0,2,1]
                // u:1 - v:3 [0,0,0,1,1]
                // u:2 - v:3 [0,0,0,0,1]
                // u:3 - v:4 [0,0,0,0,0]
                // 如果入度变为0，加入队列
                if (inDegree[v] == 0) {
                    queue.add(v);
                }
            }
        }

        // 检查是否有环（如果结果集中的节点数不等于总节点数，则存在环）
        if (result.size() != V) {
            System.out.println("图中存在环，无法进行拓扑排序");
            return new ArrayList<>();
        }

        return result;
    }

    /**
     * DFS算法实现拓扑排序
     * 思路：深度优先搜索，逆序收集结果
     */
    public List<Integer> topologicalSortDFS() {
        // 标记节点是否被访问
        boolean[] visited = new boolean[V];
        // 用于检测环
        boolean[] recStack = new boolean[V];
        // 存储拓扑排序结果（逆序）
        Stack<Integer> stack = new Stack<>();

        // 对每个未访问的节点进行DFS
        for (int i = 0; i < V; i++) {
            if (!visited[i]) {
                if (dfs(i, visited, recStack, stack)) {
                    System.out.println("图中存在环，无法进行拓扑排序");
                    return new ArrayList<>();
                }
            }
        }

        // 将栈中的结果转为列表
        List<Integer> result = new ArrayList<>();
        while (!stack.isEmpty()) {
            result.add(stack.pop());
        }

        return result;
    }

    /**
     * DFS辅助函数
     * @return 如果发现环则返回true，否则返回false
     */
    private boolean dfs(int v, boolean[] visited, boolean[] recStack, Stack<Integer> stack) {
        // 如果节点在当前递归栈中，说明存在环
        if (recStack[v]) {
            return true;
        }

        // 如果节点已被访问，直接返回
        if (visited[v]) {
            return false;
        }

        // 标记当前节点为已访问，并加入递归栈
        visited[v] = true;
        recStack[v] = true;

        // 递归访问所有相邻节点
        for (int neighbor : adj.get(v)) {
            if (dfs(neighbor, visited, recStack, stack)) {
                return true;
            }
        }

        // 从递归栈中移除当前节点
        recStack[v] = false;
        // 将当前节点加入结果栈
        stack.push(v);

        return false;
    }

    // 测试
    public static void main(String[] args) {
        // 创建一个有5个节点的图
        TopologicalSort graph = new TopologicalSort(5);

        // 添加边，构建图
        graph.addEdge(0, 1);
        graph.addEdge(0, 2);
        graph.addEdge(1, 3);
        graph.addEdge(2, 3);
        graph.addEdge(3, 4);

        System.out.println("使用Kahn算法的拓扑排序结果:");
        List<Integer> kahnResult = graph.topologicalSortKahn();
        System.out.println(kahnResult);

        System.out.println("使用DFS算法的拓扑排序结果:");
        List<Integer> dfsResult = graph.topologicalSortDFS();
        System.out.println(dfsResult);

        // 测试一个有环的图
        TopologicalSort cyclicGraph = new TopologicalSort(3);
        cyclicGraph.addEdge(0, 1);
        cyclicGraph.addEdge(1, 2);
        cyclicGraph.addEdge(2, 0); // 形成环

        System.out.println("有环图的Kahn算法结果:");
        List<Integer> cyclicKahnResult = cyclicGraph.topologicalSortKahn();
        System.out.println(cyclicKahnResult);
    }
}

资料

拓扑排序（Topological Sorting）有向图的拓扑排序——DFS