数据结构和算法
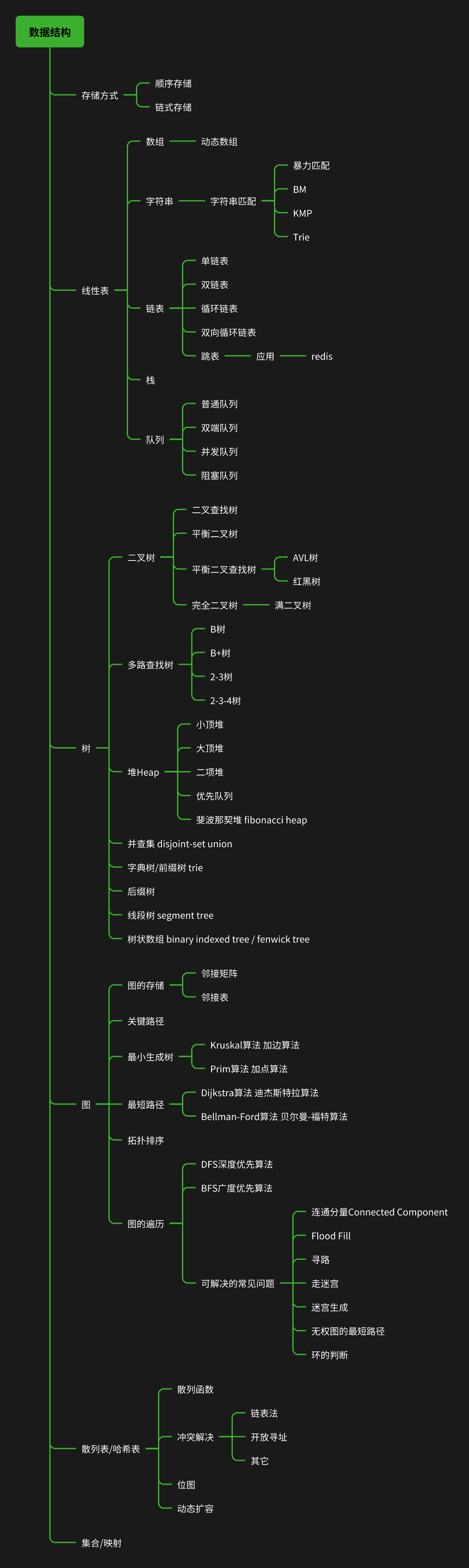
数据结构
线性表
链表 | 单链表 | 双链表 | 循环链表 | 双向循环链表 | 跳表
队列 | 普通队列 | 双端队列 | 并发队列 | 阻塞队列
树
多叉树 | 字典树/前缀树
图
图的存储 邻接矩阵无向图 | 邻接表无向图 | 邻接矩阵有向图 | 邻接表有向图
最短路径Disjktra | BellmanFord
拓扑排序 | 关键路径 | 图的遍历
散列表
复杂度

导图
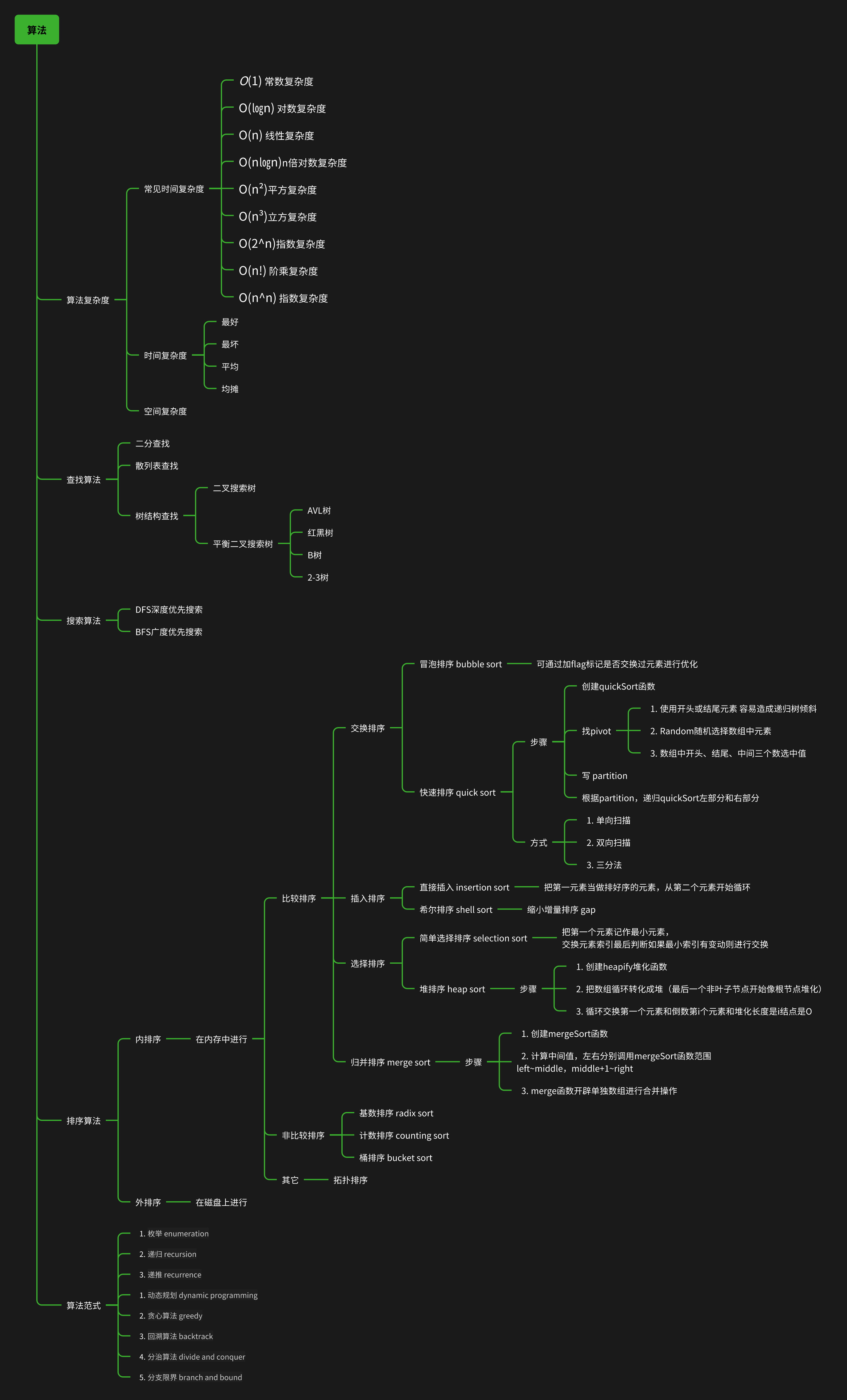
算法
算法介绍
算法刷题
方法 | 刷题 | 力扣 leetcode | 领扣 lintcode
排序算法
归并排序归并排序
其他排序拓扑排序
查找算法
搜索算法
其它算法
位运算 | 布隆过滤器 | 大数据和空间限制 | 一致性哈希算法 | LRU Cache
算法范式
思想基础
1. 递归 recursion
2. 递推 recurrence
3. 枚举 enumeration
算法思想
1. 动态规划 dynamic programming
2. 贪心算法 greedy
3. 回溯算法 backtrack
4. 分治算法 divide and conquer
5. 分支限界 branch and bound
导图
问题 test
介绍红黑树的特点和应用场景
特点
- 高度平衡:任何路径上的黑色节点数相同。
- 插入和删除操作:保证树的高度平衡,最坏情况下的复杂度为 O(log n)。
- 颜色属性:每个节点有两个属性,一个是键值,另一个是颜色(红色或黑色)。
应用场景
- 文件系统:用于维护文件和目录的层次结构。
- 数据库索引:构建索引以支持快速查找。
- 语言编译器:用于符号表管理。
总结
表格 还在加载中,请等待加载完成后再尝试复制
简述跳表(Skip List)的数据结构和优势
数据结构
- 层级结构:每个节点包含多个指向前方节点的指针。
- 概率分布:指针的数量根据概率分布决定。
- 索引结构:通过索引结构快速定位目标节点。
优势
- 插入和删除操作:平均时间复杂度为 O(log n)。
- 查找操作:平均时间复杂度为 O(log n)。
- 易于实现:相比于红黑树等自平衡二叉树更容易理解和实现。
总结
表格 还在加载中,请等待加载完成后再尝试复制
谈谈布隆过滤器(Bloom Filter)的原理和用途
原理
- 位数组:使用一个很长的二进制向量和一系列随机映射函数。
- 插入操作:将元素通过不同的哈希函数映射到位数组中。
- 查询操作:通过相同的哈希函数检查位数组中的相应位。
用途
- 数据去重:用于判断某个元素是否出现过。
- 缓存过滤:在缓存系统中过滤掉不需要加载的数据项。
- 数据库查询优化:在进行数据库查询前进行预筛选。
总结
表格 还在加载中,请等待加载完成后再尝试复制
解释线段树(Segment Tree)的数据结构和应用
数据结构
- 完全二叉树:通常使用数组表示。
- 叶子节点:代表原始数组中的元素。
- 非叶子节点:代表区间的信息。
应用
- 区间查询:快速查询给定区间内的信息。
- 区间更新:快速更新给定区间内的信息。
- 动态规划:用于动态规划问题中的区间信息。
总结
表格 还在加载中,请等待加载完成后再尝试复制
描述并查集(Union-Find)的数据结构和算法
数据结构
- 森林结构:一组树的集合,每棵树代表一个集合。
- 根节点:每个集合的代表元素。
算法
- 查找操作:找到元素所属集合的代表元素。
- 合并操作:将两个集合合并为一个集合。
- 路径压缩:在查找过程中优化查找路径。
总结
表格 还在加载中,请等待加载完成后再尝试复制
谈谈字典树(Trie)的结构和应用
结构
- 根节点:通常为空节点。
- 子节点:每个子节点代表一个字符。
- 路径:从根节点到某个节点的路径代表一个字符串。
应用
- 前缀匹配:快速查找具有共同前缀的字符串。
- 单词建议:提供基于用户输入的单词建议。
- IP路由选择:用于网络中的路由选择。
总结
表格 还在加载中,请等待加载完成后再尝试复制
解释斐波那契堆(Fibonacci Heap)的特点和用途
特点
- 斐波那契堆:一种特殊的最小堆。
- 节点结构:每个节点包含一个子堆。
- 合并操作:合并两个堆只需要将它们链接在一起。
用途
- 图算法:在 Dijkstra 算法和 Prim 算法中优化性能。
- 优化问题:用于求解某些优化问题。
总结
表格 还在加载中,请等待加载完成后再尝试复制
简述 AVL 树的平衡调整策略
平衡条件
- 平衡因子:每个节点的左子树和右子树的高度差不超过 1。
- 旋转操作:通过四种旋转操作来调整不平衡的情况。
旋转操作
- LL旋转:当左子树的高度大于右子树的高度,并且左子树的左子树的高度也更大。
- RR旋转:当右子树的高度大于左子树的高度,并且右子树的右子树的高度也更大。
- LR旋转:当左子树的高度大于右子树的高度,但左子树的右子树的高度更大。
- RL旋转:当右子树的高度大于左子树的高度,但右子树的左子树的高度更大。
总结
表格 还在加载中,请等待加载完成后再尝试复制
谈谈后缀树(Suffix Tree)的概念和应用
概念
- 后缀:字符串的所有可能的后缀。
- 后缀树:用于存储字符串所有后缀的树形结构。
应用
- 字符串匹配:快速查找字符串中的模式。
- 生物信息学:用于 DNA 序列分析。
- 文本处理:用于文本搜索和索引构建。
总结
表格 还在加载中,请等待加载完成后再尝试复制
解释块状数组(Block Array)的数据结构和优势
数据结构
- 固定大小的块:数组被划分成固定大小的块。
- 索引结构:通过索引结构快速定位到特定的块。
优势
- 内存对齐:改善内存访问效率。
- 缓存友好:提高缓存命中率。
- 并行处理:适合并行处理和大规模数据操作。
总结
表格 还在加载中,请等待加载完成后再尝试复制
描述伸展树(Splay Tree)的操作和特点
特点
- 自调整二叉搜索树:伸展树是一种自调整的二叉搜索树。
- 频繁访问的节点靠近根节点:通过旋转操作使得最近被访问的节点更接近树的根节点。
- 高效查询和更新:伸展树在查询和更新操作上表现出良好的性能。
基本操作
- 查找操作:通过比较节点值来查找目标节点。
- 插入操作:插入新节点后,通过一系列旋转操作将新节点提升至根节点位置。
- 删除操作:删除节点后,需要通过旋转操作来重新平衡树。
旋转操作
- Zig操作:单旋,适用于新节点是其父节点的左子节点或右子节点。
- Zig-Zig操作:双旋,适用于新节点是其父节点的左子节点的左子节点或右子节点的右子节点。
- Zig-Zag操作:双旋,适用于新节点是其父节点的左子节点的右子节点或右子节点的左子节点。
总结
表格 还在加载中,请等待加载完成后再尝试复制
谈谈左偏树(Leftist Tree)的数据结构和应用
数据结构
- 二叉堆:左偏树是一种特殊的二叉堆。
- 左偏性质:每个节点的左子树的权重至少不小于其右子树的权重。
- 节点结构:每个节点包含一个权重值,代表该节点及其子树的权重总和。
应用
- 优先队列:左偏树可以用来实现高效的优先队列。
- 动态集合:用于动态集合的操作,例如合并两个集合。
总结
表格 还在加载中,请等待加载完成后再尝试复制
解释二项堆(Binomial Heap)的性质和操作
性质
- 二项系数:每个二项堆的节点数都是2的幂次。
- 唯一性:对于给定的节点数,二项堆的形状是唯一的。
- 层次结构:二项堆由一系列二项树组成,每个二项树的节点数为2^k。
基本操作
- 合并操作:合并两个二项堆,保持其二项系数性质。
- 提取最小元素:从二项堆中提取最小元素。
- 减少键操作:修改某个节点的键值,使其变得更小。
总结
表格 还在加载中,请等待加载完成后再尝试复制
简述配对堆(Pairing Heap)的特点和算法
特点
- 灵活的结构:没有固定的形状限制。
- 简单高效:实现非常简单,同时具有很好的实际性能。
- 懒惰合并:配对堆倾向于延迟合并操作,直到必要时才执行。
算法
- 插入操作:创建一个新的节点,然后与当前堆进行合并。
- 提取最小元素:移除最小元素后,将剩余的子堆重新配对合并。
- 减少键操作:修改节点的键值,然后上浮该节点以保持堆的性质。
总结
表格 还在加载中,请等待加载完成后再尝试复制
谈谈拓扑排序(Topological Sort)的算法和应用
算法
- 入度计数:计算每个顶点的入度。
- 零入度顶点:选择入度为0的顶点作为起点。
- 移除顶点和边:移除选定的顶点及其出边,更新其他顶点的入度。
应用
- 任务调度:安排有依赖关系的任务执行顺序。
- 编译器优化:用于确定指令的最优执行顺序。
- 软件工程:确定模块之间的依赖关系。
总结
表格 还在加载中,请等待加载完成后再尝试复制
解释关键路径(Critical Path)算法的原理和用途
原理
- 最早开始时间和最晚完成时间:计算每个任务的最早开始时间和最晚完成时间。
- 最长路径:关键路径是项目网络图中最长的路径,决定了项目的最短完成时间。
用途
- 项目管理:用于识别项目中最关键的任务序列。
- 资源分配:优化资源在关键任务间的分配。
- 风险评估:评估项目延期的风险。
总结
表格 还在加载中,请等待加载完成后再尝试复制
描述最短路径算法,如 Dijkstra 算法和 Floyd 算法
Dijkstra 算法
- 贪婪策略:每次选择距离最短的未访问节点。
- 优先队列:使用优先队列来选择下一个访问的节点。
- 松弛操作:更新节点的距离值。
Floyd 算法
- 动态规划:通过逐步增加中间顶点的数量来计算所有顶点对之间的最短路径。
- 三维数组:使用一个三维数组来存储路径信息。
- 迭代更新:通过迭代更新顶点之间的路径长度。
总结
表格 还在加载中,请等待加载完成后再尝试复制
谈谈最小生成树算法,如 Prim 算法和 Kruskal 算法
Prim 算法
- 贪婪策略:每次添加与当前生成树连接的最小权重边。
- 优先队列:使用优先队列来选择下一个加入生成树的边。
- 邻接矩阵:适用于密集图。
Kruskal 算法
- 排序边:按照权重从小到大排序所有的边。
- 并查集:使用并查集数据结构来检测环路。
- 贪心选择:每次选择不会形成环的最小权重边。
总结
表格 还在加载中,请等待加载完成后再尝试复制
解释贪心算法(Greedy Algorithm)的概念和应用
概念
- 局部最优选择:在每一步都做出当前看来最好的选择。
- 全局最优解:期望这些局部最优选择能够导出问题的全局最优解。
应用
- 活动选择问题:选择尽可能多的互不冲突的活动。
- 最小生成树:构建图的最小生成树。
- 霍夫曼编码:用于数据压缩的编码方法。
总结
表格 还在加载中,请等待加载完成后再尝试复制
简述动态规划(Dynamic Programming)的思想和应用
思想
- 重叠子问题:将原问题分解为多个较小的子问题。
- 最优子结构:原问题的最优解可以通过子问题的最优解来构造。
- 记忆化:保存子问题的解以避免重复计算。
应用
- 背包问题:解决物品的选择问题。
- 编辑距离:计算两个字符串之间的差异。
- 最长公共子序列:找出两个序列的最长公共子序列。
总结
表格 还在加载中,请等待加载完成后再尝试复制
数组和链表的区别
数组
- 定义:数组是一种线性的数据结构,其中的元素在内存中是连续存放的。
- 访问方式:可以通过索引直接访问任何一个元素,时间复杂度为O(1)。
- 插入和删除:在数组中插入或删除元素通常需要移动大量的元素以保持连续性,时间复杂度为O(n)。
- 空间开销:除了数据本身,还需要额外的空间开销较小,只包含少量的元数据。
- 适用场景:适合于需要快速随机访问的场景。
链表
- 定义:链表也是一种线性的数据结构,但是其中的元素不是连续存放的,而是通过指针链接起来。
- 访问方式:需要从头节点开始逐个遍历,时间复杂度为O(n)。
- 插入和删除:在链表中插入或删除元素只需要改变相应的指针即可,时间复杂度为O(1)。
- 空间开销:除了数据本身,还需要额外的空间来存储指针信息。
- 适用场景:适合于需要频繁进行插入和删除操作的场景。
比较
表格 还在加载中,请等待加载完成后再尝试复制
二叉树的深度优先遍历和广度优先遍历的具体实现
深度优先遍历 (DFS)
- 前序遍历:根节点 → 左子树 → 右子树
- 中序遍历:左子树 → 根节点 → 右子树
- 后序遍历:左子树 → 右子树 → 根节点
递归实现
public void preOrder(TreeNode root) {
if (root != null) {
System.out.print(root.val + " ");
preOrder(root.left);
preOrder(root.right);
}
}
public void inOrder(TreeNode root) {
if (root != null) {
inOrder(root.left);
System.out.print(root.val + " ");
inOrder(root.right);
}
}
public void postOrder(TreeNode root) {
if (root != null) {
postOrder(root.left);
postOrder(root.right);
System.out.print(root.val + " ");
}
}
非递归实现
public void preOrderIterative(TreeNode root) {
if (root == null) return;
Stack<TreeNode> stack = new Stack<>();
stack.push(root);
while (!stack.isEmpty()) {
TreeNode node = stack.pop();
System.out.print(node.val + " ");
if (node.right != null) stack.push(node.right);
if (node.left != null) stack.push(node.left);
}
}
广度优先遍历 (BFS)
- 层序遍历:按照树的层次顺序遍历节点
实现
public void bfs(TreeNode root) {
if (root == null) return;
Queue<TreeNode> queue = new LinkedList<>();
queue.offer(root);
while (!queue.isEmpty()) {
TreeNode node = queue.poll();
System.out.print(node.val + " ");
if (node.left != null) queue.offer(node.left);
if (node.right != null) queue.offer(node.right);
}
}
详细讲堆的结构
堆的定义
- 完全二叉树:堆是一种特殊的完全二叉树。
- 最大堆:每个节点的值都不小于其子节点的值。
- 最小堆:每个节点的值都不大于其子节点的值。
特性
- 数组表示:堆可以用数组来表示,其中第i个节点的左子节点位于2i+1,右子节点位于2i+2,父节点位于(i-1)/2。
- 堆属性:最大堆或最小堆的性质保证了根节点总是堆中最大的或最小的元素。
堆操作
- 插入操作:将新元素添加到堆的末尾,然后通过上浮操作维持堆的性质。
- 删除操作:移除根节点,并将最后一个元素放置在根位置,然后通过下沉操作恢复堆的性质。
示例
最大堆
数组表示:[9, 5, 6, 2, 3]
树形表示:
深色版本
9 / \ 5 6 / \ 2 3
堆和树的区别
表格 还在加载中,请等待加载完成后再尝试复制
堆和栈在内存中的区别是什么?
数据结构方面
- 堆:堆是指程序运行时动态分配的内存区域,用于存储动态分配的对象。
- 栈:栈是指程序运行时静态分配的内存区域,用于存储函数调用的局部变量和函数参数。
实际实现方面
- 堆:堆内存的分配和释放由程序员控制,使用
new和delete(C++)或者new和gc(Java)来管理。 - 栈:栈内存的分配和释放由编译器自动管理,函数调用结束时自动释放。
比较
表格 还在加载中,请等待加载完成后再尝试复制
Java语言实现链表逆序代码
public class ListNode {
int val;
ListNode next;
ListNode(int x) { val = x; }
}
public ListNode reverseList(ListNode head) {
ListNode prev = null;
ListNode current = head;
ListNode next;
while (current != null) {
next = current.next;
current.next = prev;
prev = current;
current = next;
}
return prev;
}
讲一下对树,B+树的理解
树
- 定义:树是一种非线性的数据结构,它由一个根节点和若干子树组成。
- 特性:树中的节点可以有任意数量的子节点。
- 应用:文件系统的目录结构、XML文档等。
B+树
- 定义:B+树是一种自平衡的树数据结构,常用于数据库和文件系统的索引。
- 特性:
- 所有的叶子节点都在同一层。
- 内部节点只用于导航,而叶子节点包含实际的数据记录。
- 支持高效的范围查询和排序查询。
- 应用场景:数据库索引、文件系统索引等。
讲一下对图的理解
图的定义
- 定义:图是由一组节点(顶点)和一组边组成的数学结构。
- 分类:
- 无向图:边没有方向。
- 有向图:边有方向。
- 加权图:边具有权重。
- 表示:
- 邻接矩阵
- 邻接列表
图的应用
- 网络分析:社交网络分析、互联网路由。
- 最短路径问题:交通路线规划、网络通信。
- 图着色问题:调度、地图着色。
判断单链表成环与否
Floyd’s Cycle-Finding Algorithm (龟兔赛跑)
public boolean hasCycle(ListNode head) {
if (head == null || head.next == null) {
return false;
}
ListNode slow = head;
ListNode fast = head.next;
while (fast != null && fast.next != null) {
if (slow == fast) {
return true; // 发现环
}
slow = slow.next;
fast = fast.next.next;
}
return false; // 未发现环
}
资料
数据结构-浙江大学 | 黄浩杰 | 极客时间算法训练营 覃超 | 程序员代码面试指南 左程云
干货整理 算法+数据结构+计算机基础(计网+MySQL+操作系统)优质文章,错过了血亏
https://leetcode-cn.com/problems/best-time-to-buy-and-sell-stock/solution/yi-ge-fang-fa-tuan-mie-6-dao-gu-piao-wen-ti-by-l-3/ https://baike.baidu.com/item/%E5%8D%A1%E7%89%B9%E5%85%B0%E6%95%B0 https://leetcode-cn.com/problems/longest-common-subsequence/solution/a-fei-xue-suan-fa-zhi-by-a-fei-8/ https://zhuanlan.zhihu.com/p/30959069 https://wizardforcel.gitbooks.io/the-art-of-programming-by-july/content/02.06.html https://www.jiuzhang.com/course/71/ https://www.cxyxiaowu.com/672.html https://zhuanlan.zhihu.com/p/126546914 https://blog.csdn.net/qq_36903042/article/details/100798101 https://www.cnblogs.com/zknublx/p/5885840.html https://www.cnblogs.com/jslee/p/3431046.html https://shimo.im/docs/3xY8Wd9Chv6c9k3r/read